Joining Dots

"The origins of graph theory are humble, even frivolous" - Norman L Biggs

Graphs, and I don't mean visual ones I mean the ones where we can connect lots of points. This is a mathematically important study because when you stop and think about it lots of things are about the connection of lots of things. Computer networks like the one you are reading this on rely on this. Think about it with a network every computer doesn't need to know how to connect to every other computer it just has to have a method of asking for that data from other computers and if they don't know they can ask the other computers and so on and so on until you get the correct data.

Types of graphs:

A good rule of thumb if you can think of it as a network you can consider it a graph. A graph includes Nodes, Edges, and Vertexes.

-Neural Networks include a single directed graph that feeds forward then propagates the error backward.

-Social Networks can be analysed as a graph where the individuals are nodes and the connections are vertexes. Interestingly if we take society away from the network then we can see the way people interact can be seen as a network. Human influence absent the computer tends to follow the rules associated with networks with central thought leaders, cliques, and groups mirroring the way computers are networked.

-Disease propagation can be seen as a graph where individuals are nodes and the vectors are vertexes that pass the disease.

-Biology for food webs.

-Genomics for analysing genetics often involves arranging the data into a graph.

-Physics and chemistry for modelling molecule bonds.

-Mazes can surprisingly be built algorithmically.

-Pathfinding in games

-And of course computer networks...

So this blog is to serve as an introduction to graph theory, I am going to go over how many different ways there are to join a random selection of dots. This might sound a little contrived but I found this was the easiest way to get my head around the problem and while I have in the past used graph-based data structures in code I haven't given any thought about the theory. But first some actual definitions for graph theory.

Graph Theory

There are some ideas that I found useful from graph theory. Though I think I am far away from being an expert these are some things that I picked up that improved my thinking. I think a starting point to understand graphs better is to increase my vocabulary.

-Directed versus undirected graph: A directed graph can only go in one direction, and an undirected graph (also called connected) you can move in any direction. In a directed graph (i.e. remember one way) if the graph meets up with itself it becomes a cycle but if it doesn't it is likely to be a tree. A graph without cycles is called an acrylic graph. A connected graph without cycles is called a Tree.

-Edge and Node: an edge is an edge that is intuitively on the edge of the graph and a node is connected to multiple objects. Something I had not realised is it is hard to algorithmically identify edges as you parse through data upon getting to the end of a directed graph the edges will not have any further connections making it easy to test for when to stop but algorithms needed for You could not identify an edge or endpoint without tacking were previously visited. A tree edge and node are often called leaf and branch.

-Vertex the connection between two points.

-Neighbourhood: Describing the relationship of a node with other nodes, both the nodes connected to one node and any vertex connecting two nodes also connected to the starting node.

-Path: the route taken between different nodes in the network. This is important as it forms the basis of how to think about pathfinding systems which are different methodologies for evaluating which out of several paths are preferred based on some heuristic. In games, many pathfinding lists rely on several objects with adjacency lists that provide the pointers to the other data objects.

-A loop is not a cycle, in that a loop is where a node or edge has a connection back to itself. I have seen this proposed for neural networks where the neuron cycles its previous output to be a new input. This is important as it is proposed a many-stage multi-level "strange loop" is thought to be the basis of consciousness as proposed in "I Am a Strange Loop", published in 2007 by Douglas Hofstadter in Gödel, Escher, Bach.

-Clique: Surprisingly the phrase used for high school politics has a mathematical definition. In a clique, every member of the clique is adjacent i.e. linked to every other member of the clique but not to the whole population. You can see why this would be toxic if a clique managed a business or school because if the connections represented communication then they literally cannot hear the opinions from outside the clique to represent the population.

-Component: A component is a separated part of the graph that has not been connected to the wider network. While the point at which a graph becomes disconnected i.e. the line which you can draw between two components that splits them up is called a cut.

Now that is a small scratching of the surface of Graph Theory and probably the barest minimum requirement to start discussing the subject. There is far more to do with analysing graphs and data but I thought I ought to start from the basics of how many different ways could I come up with to connect up a bunch of random dots and what sort of things would that teach me about graph theory.

Building Algorithms

Also, small world networks show to use for neural networks. The pure magazine did an article on this here The mathematical shapes in your brain | plus.maths.org. So I decided I had no idea how to build a graph beyond the normal methods of python creating a dictionary of dictionaries or a class object with a list of other class objects inside I haven't given any thought to how to link together objects into a graph.

So I decided to create some different code to think through how might start linking different points together. So I looked into a massive oversimplification of graph theory. The task I set myself was to write a set of algorithms that connected a random set of points into a network. What the points are could be changed as long as they have an X and Y dimension.

Though I didn't start with that and worked up with it. The below is produced from every point only connecting with two other objects and picking the two closest. You can see that this doesn't guarantee that everything will be corrected you can see that several free-floating components are connected to the side. This would be the minimum effort required to create a graph that well looks like a graph.

If by the way, you were to connect the two furthest distances you would get the next graph.

If we connected to the furthest distance we get the below. Note there do not appear to be any constructs. Everything appears to be connected and while you probably wouldn't want those travel times unlike the previous you probably could get anywhere in the network. Though I'd probably vote against this network architecture as it maximizes distance and steps.

So we find that the two methods that come to mind of connect to closest or connect to farthest don't create connected networks, if this was a social network the first would mean you only where friends with people directly in their family, and the latter would require you to send messages via someone in the arctic to eventually get it passed to your brother sitting next to you.

Graphs are more complicated than you might initially think.

Random Graphs

So if we were to think about creating graphs we at first might want to find a way to ensure we avoid creating the components in the above where we connected to the closest point. So what happens if we created some of the connections at random and then kept out of the random connections the closest we get a network like the below.

Does this not seem a lot more natural? If I told you the below was the graph of relationships in a small town you would be forgiven for believing me. Therefore this is the first interesting insight from graph theory to human experiences in that natural networks often include some elements of randomness. People aren't algorithms you find connections between people of two warring nations often enough to conclude people often behave contrary to neat algorithms.

This is an interesting insight because it suggests that an inefficient but doable method of connecting a graph involves an element of randomness. This follows because it only takes a single crossover point between two components to connect them.

Though what is notable absence is the appearance of cliques, We might if this was normal data expect to see super hubs of highly connected individuals. The rate that highly clustered groups appear is sometimes called the clustering coefficient. Why cliques might form in a network is obvious when you think about social media in that any new addition to the network is simply more natural to be or seek a connection with someone already highly connected in the network.

Though even within computer networks we see a small number of hyper-connected hub nodes such as major DNS servers that behave in the same way so much so that it seems a truism of networks that what we tend towards is small hyper-connected nodes that play a vital role for the larger network.

There is a whole subset of graph theory called percolation theory that deals with how and where people or objects can get added to a network and the impacts of adding new objects to the graph will have.

So how do we randomly produce a graph that will look more natural and what will that tell us about the maths that underlie graphs?

Barabási_Albert - starting to think of graphs as networks

So where should we start thinking about social media networks, friend networks we might start with algorithms like the Barabási_Albert algorithm that works so that any new addition to a system is weighted to join to a node with existing connections. My implementation of the algorithm is below but you can also see a picture of it on Wikipedia.

So given that we are to suggest that the Barabási_Albert algorithm represents a more natural pattern for explaining how networks form what can we derive from this. Well notice below there are cliques and several hyper-connected individual nodes which are connected more than others. This is because nodes with connections are more likely to gain more connections and become a hub.

Another suggestion we can derive from this algorithm is that the first individual node in the network may have a greater chance if they are lucky enough to start getting new connections they will rapidly get further more connections, though with the below implementation if an individual node is first and fails to gain initial starting connections may struggle to then get further connections. That

So it is worth stopping and thinking if this is a model of how more natural social networks form following similar rules then some individuals may monopolize control over a network and certain individuals might be excluded. This is quite chilling if we think this represents the natural development of normal social networks.

If this is a natural algorithm for how social networks work then the conclusion is that it is naturally beneficial for a small number of initial founders, it discriminates against a set of unconnected nodes (in this case people), and as it grows more power and centrality is given to the small number of founders.

Another insight is that this process also creates random and bizarre inefficiencies. If you look below there are plenty of places that are right next door to each other in terms of space but share no connection and this happens in multiple places in the network.

That is scary if you thought greater connectivity meant greater influence on the network because if you were the excluded or ignored individual or group this process that creates this network is random a few individuals are very connected and influential over the system but the reason might be random and not merit-based.

Though it is worth considering why that might be an efficient communication method for computers in a network. As in the above, we created two models connected to the closest and connect to the furthest and we ended up with two broken networks. If you look below and ignore the unconnected you can see why a clique (in the mathematical sense) is highly efficient for passing information between nodes as the paths to get anywhere in the greater network is quite short. i.e. if I start at any point it doesn't appear to be lots of hops to get to the next location (think train stations).

Whether this is a computer network, a social network, a train network, or anything else it seems an efficient manner for information or moving stuff across a network to prefer to connect to the most centralized and connected nodes. That appears great for information though might also have unforeseen problems if your that excluded node.

This tendency is sometimes referred to as power-law where a few individual nodes represent high degrees of connectivity within the network. I should point out I don't think it has to do with power-law where the square root of the population does half the work or the 80/20 rule but maybe it does after all the brain is a network.

After all, it might be quite natural for networks to work this way... That is kind of interesting insight from graph theory that applies all over the place that I don't think gets discussed enough... And it applies to economic theories, computer networks, social networks, and all sorts of surprising things.

If it is natural is it efficient does that make it right if certain nodes are excluded? The thing about the Barabási_Albert algorithm is it seems to work for building networks it is fast but it is random. Should kind of make you think...

CODE:

def Barabási_Albert(count=500,rand=0.5):

evaluate=1
locations=[]
for i in range(count):

locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))
for loco in locations:

if not locations[i] is loco:

#print(((2+len(locations[i].connections))/evaluate))
if random.random() < ((2+len(locations[i].connections))/evaluate):

evaluate+=1
locations[i].add_connection(loco)

return locations

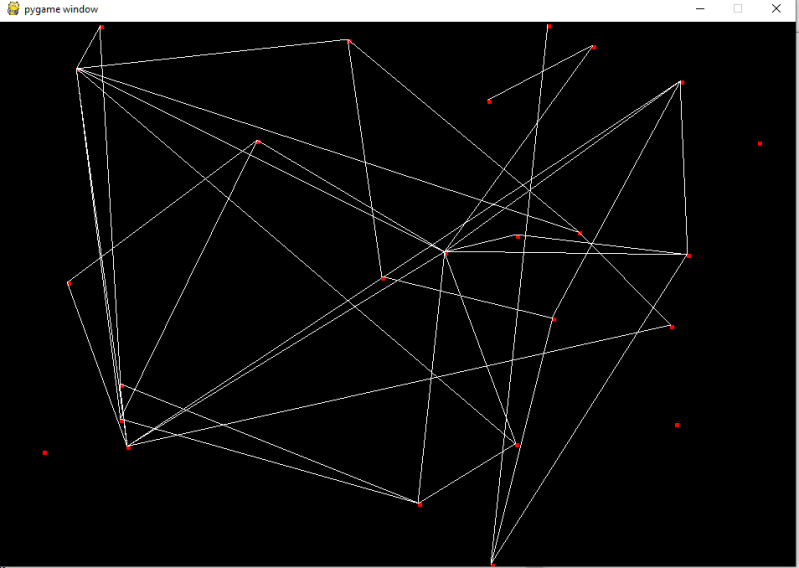
I made my own...

Though random doesn't have to be decided per connection. Nor do connections have to be calculated based randomly. The below was a heuristic-based algorithm that includes a fitness score per node and a value that mediates how big the clusters and influences should be. Over its local area and how regular or rare high influence nodes should be. Regardless low influence nodes do connect aren't excluded and influence the network.

I don't know why but I quite like it. I have always been toying with an economics game and wasn't sure how to go about randomly creating a world map. I still have some time to go but below is the candidate for connecting up the trade network once that world is produced. I think if I ran this over a Perlin noise generated world it could do a quite good representation of the underlying trade networks.

The heuristic uses a element of randomness I can't pretend the specific locations of the main nodes aren't random but I can imagine a way to shift it into finding network centres using K-means and work back of that. And from what I can tell its this method that is the most "natural" of the methods that I worked through.

In the most natural networks connections are not arbitrary they have centralised hubs that help with information processing and redundant links. And that is an interesting insight the random models have no redundancy the above random models if suffered a loss of a major node will likely be compromised. The below has the best of both worlds with centralised nodes and redundant secondary paths.

I felt like that would be a better network based on the fitness value it has highly clustered centralized nodes that allow efficient passing of information but doesn't exclude anything. I think that is an interesting insight you can get a network by doing random things but you can't get the best network. Feels suitably profound as to the nature of things and yet wholly abstract that you might apply that truism anywhere.

Conclusion

There are plenty of things I wish were better taught at school, taxes, inflation, and how money is created is one, another is always more coding and I think I would want to add graph theory.

There is a whole host of things that were inexplainable until your taught to see them as a graph, to question how things are added and removed, and to pose questions using graphs seems a missed skill.

Why are some people more popular on social media? Graph theory. Why is the internet slow? Graph theory. Questions about supply chains? Graph theory. How do social influence and opinion propagate? Graph theory. How do I build a brain? Graph theory.

And all it was was learning the different ways you could connect up a bunch of random dots. I invite you to consider the initial quote.

"The origins of graph theory are humble, even frivolous" - Norman L Biggs

FULL CODE:

import pygame
from pygame.locals import *
import random
import math

class location:
def __init__(self,x,y):
self.x=x
self.y=y
self.connections=[]
def add_connection(self,new):
self.connections.append(new)
def prune_highest(self,min_size=2):
maxi=0
loco=0
if len(self.connections) > min_size:

for connect in range(len(self.connections)):
test=self.distance(self.connections[connect].x,self.connections[connect].y)
if test > maxi:
maxi=test
loco=connect
self.connections.pop(loco)
def prune_lowest(self,min_size=2):
maxi=10000000
loco=0
if len(self.connections) > min_size:

for connect in range(len(self.connections)):
test=self.distance(self.connections[connect].x,self.connections[connect].y)
if test < maxi:
maxi=test
loco=connect
self.connections.pop(loco)
def distance(self,x,y):
x1=(self.x-x)**2
y1=(self.y-y)**2
return math.sqrt(x1+y1)

screensize=(950,650)
screen=pygame.display.set_mode(screensize,0,32)

def prune_highest(count=500):
locations=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))

for loco in locations:
for coco in locations:
if not loco is coco:
loco.add_connection(coco)
return locations

def prune_highest_random(count=100,rand=0.5):
locations=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))

for loco in locations:
for coco in locations:
if not loco is coco:
if random.random() > 0.5:
loco.add_connection(coco)
return locations

def random_geometric(count=300,rand=0.5):
locations=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))
for loco in locations:
maxi=1
for coco in locations:
test=loco.distance(coco.x,coco.y)
if test > maxi:
maxi=test
for coco in locations:
if not loco is coco:
test=loco.distance(coco.x,coco.y)

if random.random() < (test/maxi):
loco.add_connection(coco)
return locations

def Barabási_Albert(count=25,rand=0.5):
evaluate=1
locations=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))
for loco in locations:
if not locations[i] is loco:
#print(((2+len(locations[i].connections))/evaluate))
if random.random() < ((2+len(locations[i].connections))/evaluate):
evaluate+=1
locations[i].add_connection(loco)
return locations

def set_geometric(count=320,maximum=2):
locations=[]
evaluate=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))
evaluate.append(random.random())
count=0
for loco in locations:
maxi=1
for coco in locations:
test=loco.distance(coco.x,coco.y)
if test > maxi:
maxi=test
tests=[]
to_add=[]
for coco in locations:
if not loco is coco:
test=loco.distance(coco.x,coco.y)
update=False
to_update=0
mapped=0
for t in range(len(tests)):
if tests[t] < mapped:
mapped=tests[t]
to_update=t
test=(test/maxi)-evaluate[count]
if mapped > test:
if len(tests) < maximum:
tests.append(test)
to_add.append(coco)
else:
tests[to_update]=test
to_add[to_update]=coco
for add in to_add:
loco.add_connection(add)
count+=1
return locations

def set_geometric_multi(count=500,maximum=2):
locations=[]
evaluate=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))
evaluate.append(random.random())
count=0
for loco in locations:
maxi=1
for coco in locations:
test=loco.distance(coco.x,coco.y)
if test > maxi:
maxi=test
tests=[]
to_add=[]
for coco in locations:
auto=0
if not loco is coco:
test=loco.distance(coco.x,coco.y)
update=False
to_update=0
mapped=0
for t in range(len(tests)):
if tests[t] < mapped:
mapped=tests[t]
to_update=t
test=(test/maxi)-((evaluate[count]+evaluate[count])/2)
if mapped > test:
if len(tests) < maximum:
tests.append(test)
to_add.append(coco)
else:
tests[to_update]=test
to_add[to_update]=coco
auto+=1
for add in to_add:
loco.add_connection(add)
count+=1
return locations

def set_geometric2(count=2000,maximum=2,split=3,clustering_val=0.3):
locations=[]
evaluate=[]
for i in range(count):
locations.append(location(random.randint(0,screensize[0]),random.randint(0,screensize[1])))
a=0
for i in range(split):
a+=random.random()
a/=split
evaluate.append(a)
count=0
for loco in locations:
maxi=1
for coco in locations:
test=loco.distance(coco.x,coco.y)*clustering_val
if test > maxi:
maxi=test
tests=[]
to_add=[]
for coco in locations:
if not loco is coco:
test=loco.distance(coco.x,coco.y)
update=False
to_update=0
mapped=0
for t in range(len(tests)):
if tests[t] < mapped:
mapped=tests[t]
to_update=t
test=(test/maxi)-evaluate[count]
if mapped > test:
if len(tests) < maximum:
tests.append(test)
to_add.append(coco)
else:
tests[to_update]=test
to_add[to_update]=coco
for add in to_add:
loco.add_connection(add)
count+=1
return locations

locations=set_geometric2()
red=(255,0,0)
BLACK=(0,0,0)
white=(255,255,255)

while True:
screen.fill(BLACK)
pressed_keys=pygame.key.get_pressed()
for event in pygame.event.get():
if event.type==QUIT:
exit()

for loco in locations:
pygame.draw.rect(screen,red,(loco.x,loco.y,5,5))
for connection in loco.connections:
pygame.draw.line(screen, white, (loco.x, loco.y), (connection.x, connection.y))
#loco.prune_highest()
#loco.prune_lowest()
pygame.display.update()