"Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin."—John von Neumann
I needed to create a pseudo-random number generator and regular C++ doesn't allow you to save the current state (or I haven't found out how). To do this simulation properly I wanted to be able to save the state of random number generation so the next time it ran it would reliably produce the same results and do so even if later I started adding in save features.
In this article, I will go through creating several different random number generators, the broad history, theory, and how I applied this to my work. Working through the problem of random numbers you end up realising what a headache they are for philosophers. What is randomness? Is this article random? Is random thing A more or less random than thing B? Do you mean just surprising or unexpected or unknown? can something understood or controlled by people ever really be random?
So I contemplated using arithmetic methods to produce random numbers; as John von Neumann has commented in the above quote maybe that means I might be in a state of sin. There does seem to be something to this there appears to be a philosophy behind using stochastic processes to produce random numbers that seem to have philosophical issues worth examining. When using pseudo-random number generators and by extension any form of procedural generation we end up with a philosophical question of when we say random what do we mean?
Is something random because it is just completely obfuscated from the user and appears unexpected? Is it random because the oscillations are so large as to not provide a repeat of the same events except maybe over a huge geological time scale? Is it still random if with enough analysis an individual with godlike intellect could predict the next number and therefore next event in the sequence?
Pseudorandom number generation manages to be all these things at once.
That being said for simulation modelling understanding of pseudo-random numbers is important because if one can build these oscillating and obfuscated mathematical functions then you can build simulations where you can input a seed number and then for any given simulation as long as the seed is the same and the user interacts with it in the same way they will get the same output.
Features of a pseudorandom number generator
-It starts with a seed number that sets its initial value.
-if you know its current value you can tell the next value.
-Otherwise, the values go up and down so much and repeat so infrequently as to appear random.
What do we use Randomness for?
-Casinos: the fact that many systems in a casino use pseudo-random number generators and because of the statistical methods that can be abused to try and crack pseudo-random number generators is one reason casinos have a problem with card counting and spend a lot of time and money keeping the methods of producing the numbers used in there slot machines a secret.
-Cryptography: Using encryption that starts with a random number and one that can change as the program runs make encryption more secure.
-Statistical Analysis: by simulating a process and running through various iterations we can generate a simulation and analyse its processes statistically for flaws in our logic.
-Computer Games: games in real life need dice, before pseudo-random number generators where developed machines could n
Stochastic Processes
I would argue most people understand the word stochastic in the same sense most people would use the word random when talking about computers. Though to be more precise Stochastic processes are where the next value of the object is tied in some way to previous outputs. I.e. example could be temperature might go up or down but it is highly unlikely to jump randomly up 12 degrees in the next 30 minutes (which is a real shame as I sit in a room with the heating off). By contrast, a dice real-world dice would not be considered stochastic though counterintuitively because of the way computers work a dice rolled on a computer is likely stochastic.
In computers, stochastic processes can be represented by a list (a very very huge list) of numbers. As the stochastic process proceeds it increments through this incredibly huge list and selects the next number in the list.
All the values that do exist in this list are typically called X and all the values that X can take are called system states. All the system states (all possible values of X) have a dependency on each other so if I know X1 then I can calculate X2. In practice, the maths that changes X1 into X2 creates such swings and changes in values that if you didn't know the actual maths that makes X1 into X2 you might mistake them for random numbers.
Computers make use of stochastic processes in that a computer can use the current time as the starting point for the maths and then produce the values in the sequence. Given that most users do not know the exact millisecond that the pseudo-random number generator was created, even if they could do the complicated maths, they would be unlikely to know the starting point in this massive list.
The use of this in simulations and games is that if we use a list of unrelated numbers we can generate a series of events and look at their impact. Thorvald N. Thiele in 1880 came up with the idea of Brownian motion and the random walk a process used to examine particle motion. At such a time there were no modern-day computers nor any concept of pseudo-random number generators. Therefore the methods where the use of a list of unrelated numbers used to stand in for randomness.
Without stochastic processes, we would not have methods for performing desktop investigations and paper-based analysis of many real-world processes. it also is good for games...
How does this relate to simulation theory?
Random numbers are used all over the place from encryption to games and of course, I predominantly talk about simulations. Games focus on entertainment its use of random numbers is mostly for a stand-in for dice.
There is a difference in both game theory and simulations with the idea of input randomness and output randomness. i.e. in a game, if you roll to hit when firing a weapon its output randomness the action is determined at the time of action its randomness is output, and if you generate a whole random level and set the number of hits an enemy takes to a random number it's randomness is input randomness.
Because we are used to playing games using dice and rolling the dice when we do something we tend to think in terms of output randomness though is a difference? The enemy in the example will die after a random number of hits. This was an idea that John Von Neumann came up with within his work on game theory that randomness could be designed out of a process if you had statistical information across a large enough population; both the decision in a game that a rifle hits 33% of the time and kills the target and the concept that a target has 3 lives is statistically the same outside that the later allows for a string of lucky shots each killing a target or a string of hyper unlucky shots that all miss; statistically they are the same across a large enough number of games.
Simulations are not games and I would argue that in games the point of both randomness in general and AI across the larger domain is to be as simple as possible while acting in a manner that seems intuitively correct to the player and enjoyable. AI in games is rated as more "intelligent" if it takes aggressive actions, shows simple competency, and doesn't do anything suddenly jarring with which we might conclude it is broken. Where more serious simulations start to split from games is in regards to random numbers is that games want to avoid finding disruptive behaviour and simulations seek to find them to highlight where the initial theory that the simulation was designed to explore might be wrong.
Python Random Number Generators
What follows is code that produces a pseudo-random number generator and a graph produced by the code that shows the distribution over 10,000 iterations. The first 2 are supplied only for historical context as to how the ideas around pseudo-random number generators developed.
-linear congruence generator
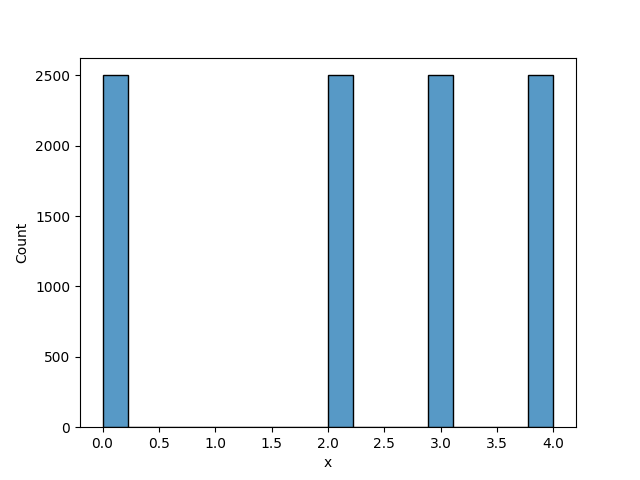
Below is Python code to show how to write a pseudo-random generator in Python. The first is the original pseudo-random number generator proposed by John Vonn Neumann and is called the Linear Congruence Generator. Now if you want to skip the code you can probably see from the graph that it only has 4 outputs [0,2,3,4]. This isn't the greatest it cycles between 4 values.
Though it sets a starting point you can mess with the input values of a,c,m, or x and it will change the behaviour. The bit that I have found in a lot of these pseudo-random number generators is the modulus function. Modulus in python is shown as a % and means give the remainder after any division i.e. 5%4=1,6%4=2,7%4=3, 8%4=0, 9%4=1.
In all cases the starting seed is X.
You couldn't use it for anything but 4 sided dice and even then you would have to interpret the 0 as a 1 and ignore that after you rolled X number you could probably guess the next value. But at least it is progress!
CODE:
#linear congruence generator
a=2
c=4
m=5
x=3
workbook={}
workbook["a"]=[]
workbook["c"]=[]
workbook["m"]=[]
workbook["x"]=[]
for i in range(1,10000):
x=(a*x+c)%m
workbook["x"].append(x)
workbook["m"].append(m)
workbook["c"].append(c)
workbook["a"].append(a)
df = pd.DataFrame(workbook)
sns.histplot(data=df, x="x")
plt.show()
Blum Blum Shub
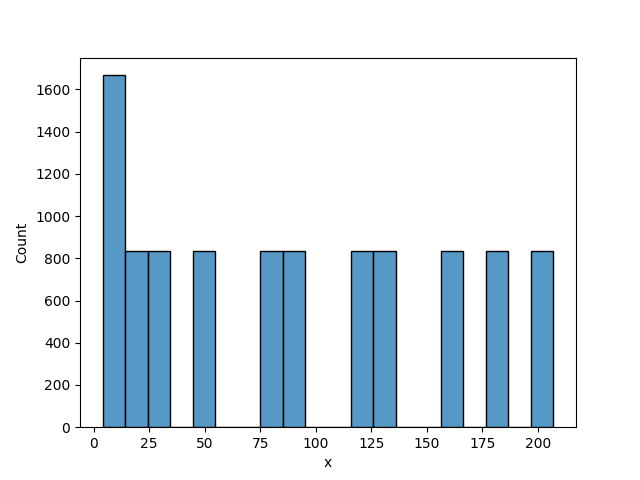
The below is another historic one useful to show the development of pseudo-random number generators. You can see from the below that it has gaps along with the 1-200 range. It is easy to look at it and see why it would have problems. You can't normalise it into a percentage because of all the gaps along the bottom.
Also for the record, I think the silly name is after the makers Lenore Blum, Manuel Blum, and Michael Shub in 1986.
CODE:
#Blum Blum Shub-
m=11*19
xi=9
workbook={}
workbook["m"]=[]
workbook["x"]=[]
for i in range(1,10000):
x=(x * x) % m
workbook["x"].append(x)
workbook["m"].append(m)
df = pd.DataFrame(workbook)
sns.histplot(data=df, x="x")
plt.show()
Learmouth Lewis Generator
There will come that will have read about that last random number generator and despaired that was developed in the '80s and question then how did we get all that 1980's RPG's which surely must have relied on some form of random number generation well in 1973 the Learmouth Lewis Generator was around.
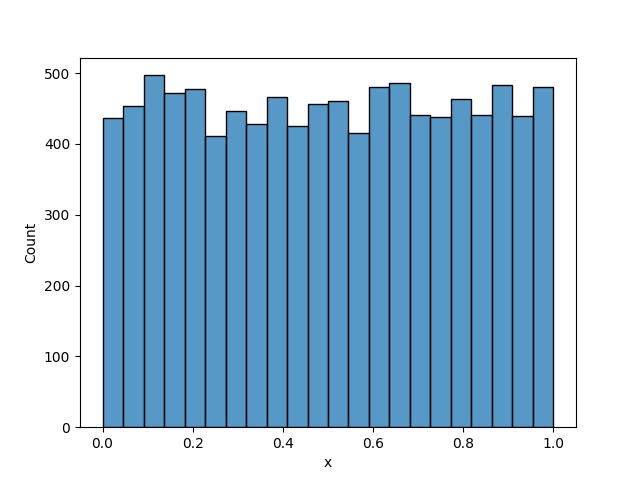
Learmouth produced values from 0-1 which allowed it to work like a percentile dice. This sounds less useful than it is as if you take any value and multiply it by Learmouth you can generate a 0-N uniform value and then by rounding it can get the straight 0-N value. i.e. if you're making a simulation or game and need to roll a six-sided dice then 6 * Learmouth() may equal 3.345 and rounding it you get a 3 making it as if you rolled dice in your game.
You can see that you're not equally likely to get every single value and the values group up slightly in the below graph. This will change slightly if you use a different starting point for X. This is where if creating a particularly involved simulation project why you might also want to check what specific method of random number generations you will use.
CODE:
#learmouth lewis generator
a=75
c=0
m=2**(31)-1
x=0.1
x2=0
workbook={}
workbook["a"]=[]
workbook["c"]=[]
workbook["m"]=[]
workbook["x"]=[]
for i in range(1,10000):
x=(a*x+c)%m
x2=x/m
workbook["x"].append(x2)
workbook["m"].append(m)
workbook["c"].append(c)
workbook["a"].append(a)
df = pd.DataFrame(workbook)
sns.histplot(data=df, x="x")
plt.show()
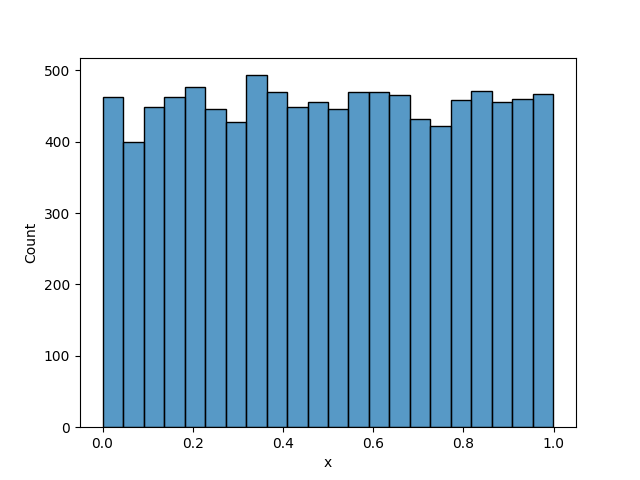
The plot changed so starting figure is 0.3 instead of 0.1. You can see there is still some uneven distribution but the values have changed. If you ran it maybe for billions or trillions of times then these statistical issues may disappear. Though this introduces the principles involved in selecting for a good random number generator involves both the period and the similarity of values output in that period.
The period in this case means the time till the generator starts repeating itself. You can therefore guess that the period is long.
the below is almost certainly ok for creating a game; though if this was a security system and we could start getting information about the distribution of past outputs we might start moving towards figuring out the original "seed" that started the random number generator. The seed is the initial value of X in the above code.
You can see why the Learmouth Lewis Generator might not be great for security reasons as random numbers are also needed for encryption, and therefore why there are a plethora of different random number generators as having multiple methods that could be used adds to security.
This follows because stochastic processes are lists of random numbers determined from the preceding random number in the series and know the method you can predict the next value.
For ultra-secure methods, you might either at the start or at certain intervals reseed your random number generator. These are called Hardware Random Number generators and whole specialist servers and processes are used to make these random numbers random. These servers can use photoelectric effects, temperatures, or nuclear decay in atoms.
If you want a further philosophical headache there are arguments over whether it is preferable (or one is more random) if the random number generation a process that is chaotic (as in defined by chaos theory) or has to be Quantum based. For true random aficionados there is always a way to be more random.
This seed or reseeding might take several forms sampling weather pressure a hidden spot is one way and in general, there are lots of different random number generation methods and servers that allow reseeding a pseudo-random number generator. Though this creates an interesting new philosophy question what is random, or what is random enough?
Lagged Fibonacci numbers
lagged Fibonacci numbers are mathematically simpler and take advantage of size differences between 32 bit and 64-bit numbers. It is mathematically faster than using the Learmouth Lewis generator. This is because it is computationally cheaper to perform addition between two values over the multiplication for
this makes it useful where speed is required. The downside is it is considered more predictable than other types.
CODE:
x0=1
x1=1
m=2**32
workbook={}
workbook["x"]=[]
workbook["m"]=[]
workbook["x0"]=[]
workbook["x1"]=[]
for i in range(10000):
x=(x0+x1)%m
x0=x1
x1=x
workbook["x"].append(x)
workbook["m"].append(m)
workbook["x0"].append(x0)
workbook["x1"].append(x1)
df = pd.DataFrame(workbook)
sns.histplot(data=df, x="x")
plt.show()
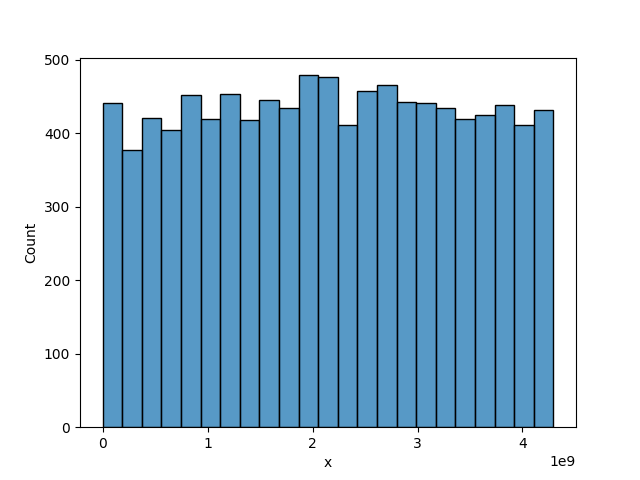
Creating my own
I was working on how to implement a random number generator for my galaxy simulation and I feel that my issues might show the benefits and problems of thinking about how to generate random numbers. The below is the lagged Fibonacci number generator, when I produced this my brain started looking for patterns in the noise of what I was seeing, and what I kept seeing was the straight lines of the yellow sun's. when you start seeing it afterward your immersion is ruined and you can't deal seriously with the idea it's real.
Whether it is art a game or a serious simulation you can see random number's matter and be they aren't truly random the method of generating them does matter.

This is the random number generator I ended up using and it is one that I wrote myself after a couple of different attempts. I spoke to my girlfriend and made the mistake of calling it pretty, she was not happy about this seeing a bunch of dots and I guess that's the point they look like a bunch of random dot's there aren't any lines to guess at you probably could imagine this was the initial map of a galaxy; give it a few cycles for gravity to tug a few planets into tighter orbits, a bit of time for atmospheres to line up and it should look alright.
What I guess I mean by pretty was I knew the amount of work that went into creating something to make it look like a bunch of random dots. Who knew randomness was well so difficult and well so precise?

Add comment
Comments