“Such heroic nonsense” – Megatron
Wrong transformer type, but I thought the quote was kind of cool and fitting. I wanted to write a whole transformer architecture from the basics with no help. It is very helpful to learn what is inside these AI, but many libraries already exist out there, and such it is a nonsense in the practical sense, though edifying and a flex to say you know how to build a whole LLm from start to finish. Therefore, I thought I would do that.
It is s useful to know about the inner workings of your car; a minimum of knowledge is useful, but obviously being a mechanic whom can change out an engine does not make you a better driver; though learning to change your engine oil will probably help look after the thing.
Short History Lesson
The transformer came to most people's attention from the 2017 paper “Attention is all you need”.
Paper found here: arXiv:1706.03762 [cs.CL]
It is especially interesting because the implementation used no memory, such as long-term term short-term memory systems or other gated memory “cells” that were common and heavily used prior to its implementation. What is interesting about the approach is that it managed to handle language tasks without memory.
Instead, the transformer used recurrent connections (i.e. connections that loop back on itself) for its sort of memory, and I believe this is why this is called “self-attention”. The original 2017 paper is believed to be the first implementation of self-attention and did not use convolution or alignment
RNN’s (recurrent neural networks). Hence, the phrase “attention is all you need” as you could expect to use the same system in place of the multi-part, encoder, decoder and memory combinations that had existed before.
Since then, the design has become a basic part of the building of large language models, which are almost entirely transformers; though other designs, both older and different, both preceded it and are in modern use.
First step in building a whole transformer
Many people are more at home with mathematical lingo than me but I wanted to write a simplified version without the word eigenvector appearing. My aim then is to;
1. Create random matrices.
2. Apply the transformer and attention block.
3. Print the output matrix
It will not perform any useful tasks because;
1. It does not have the backwards or any gradient descent learning method
2. have proper initialisation
3. does not take input data (nor implements the tokenisation).
4. Will not come near the full architecture that includes encoder and decoder systems
The aim is really to build towards intuition and understanding from writing my own code in a way that is easier to read and is only as heavy on the maths as necessary to understand the processes.
A story in 3 parts
The transformer can be thought of as 3 parts the really important one is the Matrix which is to be simple for non programmers a list of numbers but with this list you can represent a vector in maths (in fact the data object is called a vector in C++) and the most intuitive way of thinking about this is we use vectors to represent transformations or turns such that in 3d graphics it is used to spin objects.
The interesting thing is that by composing these vectors in layers, a variety of logic can be represented in the maths.
The Matrix
The matrix has a bunch of operators, but what matters is the rows_ and columns_ values that give the size of the Matrix and let us flip between treating it as a single dimension list and a 2-dimensional matrix fairly easily (it's also computationally effective in C++).
We then have two mathematical functions, softmax and layer norm. I will talk about them at the points where I use these functions.
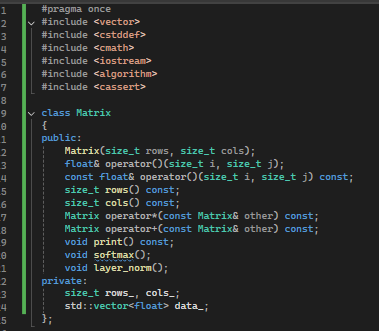
The two maths functions take the Matrix. One Softmax is central to the attention process. The other is Layer norm, which stops the error from blowing up too much and the numbers getting too large, and this is important during learning (thinks maths gets too big and pushes everything towards zero or to a stack overflow big number).
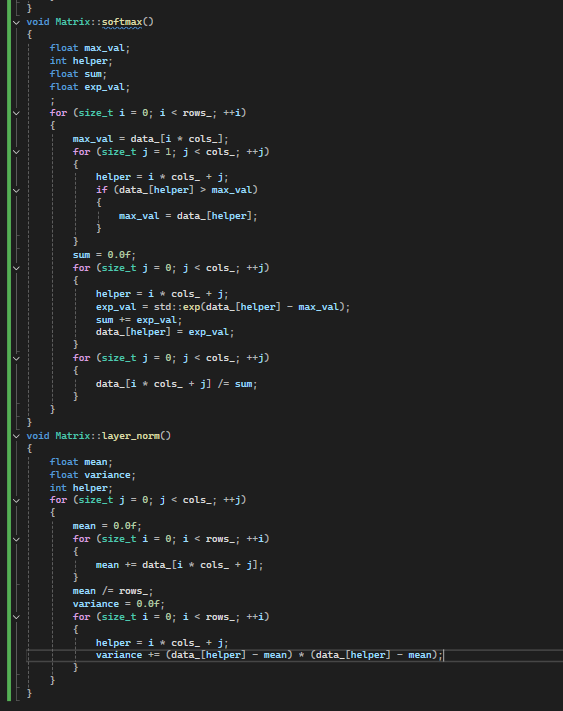
The matrix has code that, when its create,d will just take its size information for rows and columns and generates a vector (think list of numbers if not a coder) and sets them all to zero.
We create two operator overloads for plus + and multiplication *, which means when we do Matrix+Matrix or Matrix*Matrix, the code will do the maths and it looks a bit like the expected way we write in Linear Algebra and not call lots of functions because Matrix*Matrix is readable but Matrix.multiply(Matrix) can become difficult with a little scale.
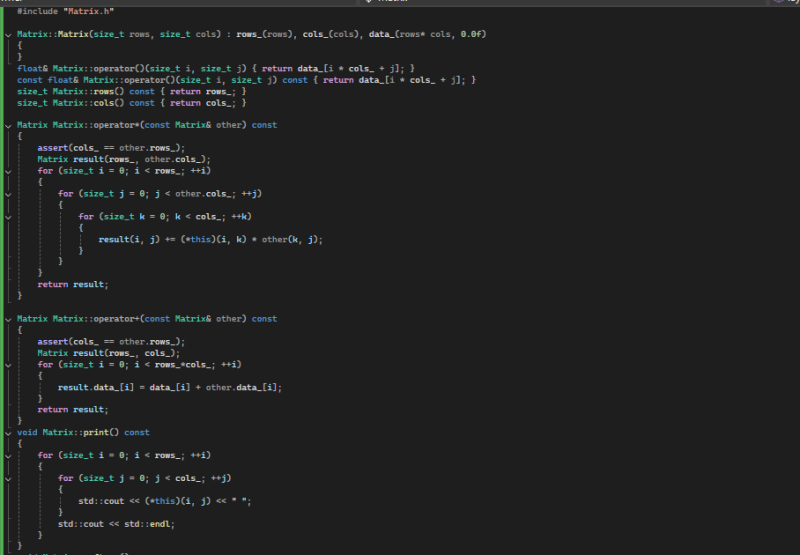
A little linear algebra goes a long way in this instance. When adding two matrices together, we move across the list of numbers, adding together the number in the same positions within both lists.
In linear algebra, it is the multiplication of one matrix by another that represents a transformation or turning. Therefore, this ends up a bit different. We need the columns of the first Matrix to be the same of the Rows by which it is multiplying because we multiply along the top and go down the rows.
This way of multiplying two matrixes works because if you had two tables of data to look up the values in the table you would turn it on its side and lookup the value. Well, this is intended to work just like this. Though the process also works well for recording a number of dimensions and
representing how you might spin it if you multiply your starting position by the transformation representing the object's turning and take the output as the new facing, you can represent an object turning in space.
You can see in the code how to use the helper function to speed up the calculation and how keeping the row and column field lets us treat a single dimensioned list and treat it as a table.
Attention
Attention is supposedly all you need, so I split it out into its own class to keep it separate. The multi headed attention and scaled dot product are the two main functions that drive a lot of the design of the transformer.
Attention works on Queries (Q) and Keys (K) and calculates a similarity score between the Query (Q) that represents what the user has input into the model (what you write in the input section of gen AI) and the Keys (the potential outputs). The actual maths is Softmax(QK)/Square root(D), where Q is the weighted Query. K is key, they are multiplied together, have the softmax activation function applied and divided by D, which is the square root of their dimensions of the matrix involved and doing so scales it correctly.
What the softmax does is turn the Q and the K into a probability distribution for the different tokens that could be output and is weighted to picking the highest.
The V means value, and it is the value, and it ensures the actual information still gets passed along (see below Score is calculated and then multiplied by V). This is meant to ensure the basic meaning of the input is passed along. If you imagine in practice, these heads are stacked on each other, the
existence of V weights, which come out of an attention head back towards the original values, so you can intuit what comes out of an attention head is the dot product of Q and K used to create a probability distribution of what is the pertinent information within the inpu,t and V reintegrates the
main Value that will be the main information captured by that attention head.
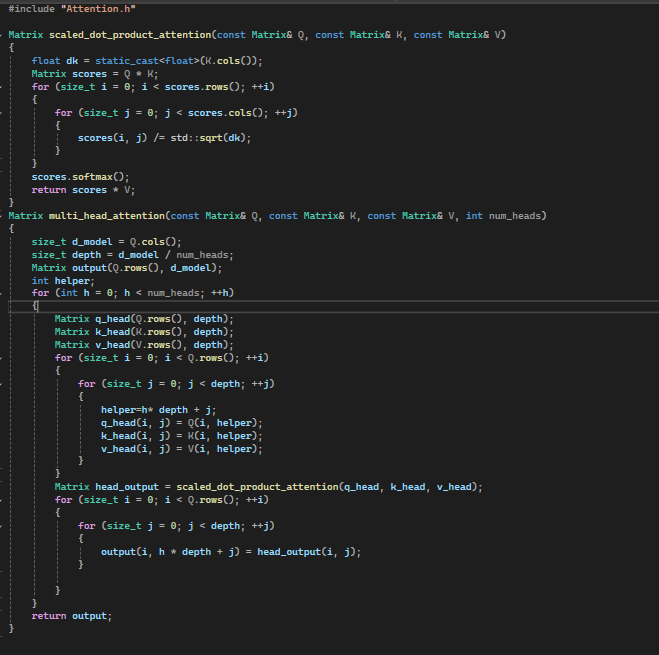
What attention lets the algorithm do is apply focus on the important aspects of a sequence at any one time. This is both true in the sense that the algorithm splits the input and applies several different transformations such that the attention system can be thought to splitting the data into
multiple subspaces (like K, Q and V above); But also in the sense that in bigger applications of it they use multiple heads and such one head might look at its input and summarise the data for long term relationships within the sentence and another might look at short term, or say a head might
describe who owns an object. The output of all these different heads is then concatenated together.
The original paper used 8 multiheaded attention. A medium-scale model might use 8-16 heads; larger models might use 32-100 heads. Where the biggest ones might use 100+ attention heads. This model takes a number for the count of heads to use, and in this case is very small and would only
build 2.
A reason why GPUs are so important in the transformer architecture is obvious from this point that such a setup produces large matrices of numbers, which can benefit from speeding up by calculating the different heads in parallel, meaning you can get faster if you use GPUs or TPUs over a regular CPU you might have on your laptop.
Many heads often stacked in layers can therefore look at the data inputted and break it up from the input data into multiple inferences and heads doing different things. Layer norm keeps the data centred around the mean while learning, so it does not end up creating very large or very small
numbers in error. This set of calculations is the basis for what they call attention.
Softmax
The star of this story is the softmax equation. All neural networks need to use activation functions that "squash" the maths down. When learning maths, if it varied exactly to match the error, we wanted to change it could very easily end up overstepping the error "Squashing" it like this lets it settle down and eventually find a good point (purposeful oversimplification).
The other thing that Softmax does is it calculates multi-class probabilities. Therefore, we can say what the probability is of given this input, whether it will be a list of different words and work out the probability of the whole list.
You can imagine why this might powerfully allow the AI to focus on the most important information from its input, creating a set of probabilities of what the AI thinks the output should be.
I am not going to deep dive the full maths, but you can pull the formulas from here.
Wikepedia: https://en.wikipedia.org/wiki/Softmax_function
Transformer
Is the overall orchestration object that calls the different functions across the system. Transformer block is where the transformer gets its name and it takes an input (called X here) and creates Q, K and V from it. These values, Q, K and V are weighted in a real version such that they are created by
Multiplying X by a weight system, and those weights are changed during learning, but I have kept that apart to implement it when I get around to the learning mechanisms.
The input itself is usually an embedding, which represents the meaning of words by translating them into numbers. This is its own area depending on tokenisation (how a sentence or block of text is split up ) and word to vector (how the tokens or words are then translated into these numbers). This is then packaged into its own matrix of a set size that can be used as the input for the maths and becomes the X in the above code, that then each of the mathematical operations take place on. I am not going to explore this area at this point.
In many architectures, these multi-heads are also stacked on top of each other, such that the output from another attention head is the input to others. This allows the model to be built in layers, and things like boolean logic, like AND, OR and XOR statements (like the ones that exist in code) in
maths can be represented by the interaction of the maths across multiple layers. If you think about it simply by sequentially pushing a number downwards then the output of a lower layer can only activate and meaningfully change the maths in upper layers if there is more of them (thereby
working like a AND gate) while if in learning the matrix pushes into larger numbers will activate the same response if any of a range of numbers from an input are received (thereby being like a OR gate). The layered matrix transformations can represent not just turns but even the types of
logic in very similar ways to how you basic computer or code runs; and with optimisation, this logic can be learned or inferred.
With enough layers, something complicated like a computer program with its AND OR gates that exist in a CPU could be represented mathematically and learne,d is the conjecture, and one that I think LLM’s show work pretty well.
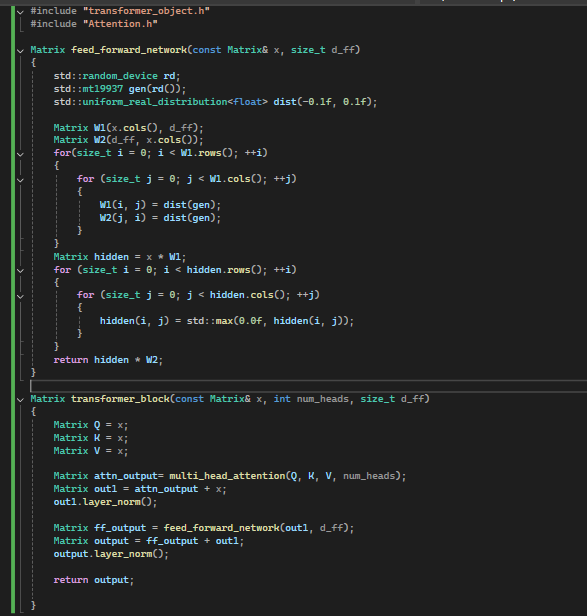
Main
From here, it will create the parts of the transformer and spit out its output to the terminal. This process is just what they would call the “forward pass” and is just the process that produces the output in a LLM and does not include the process whereby the model learns.
The C++ main looks like this.
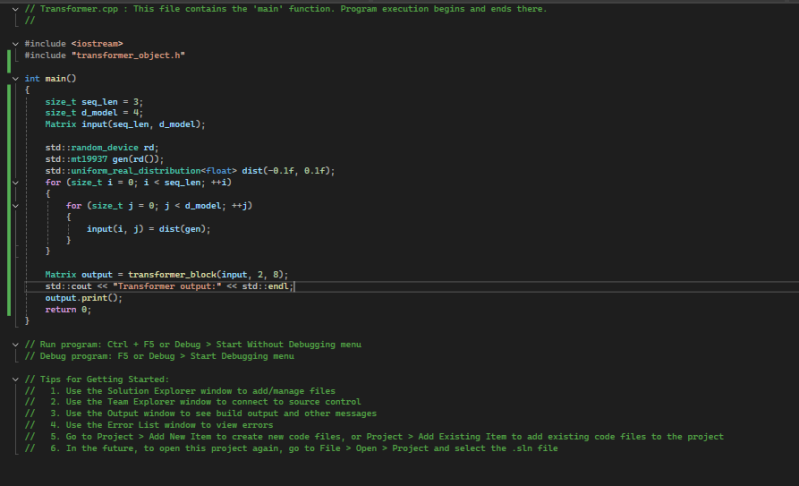
One more time from the top
In main, we create a Matrix with columns 3 and rows 4. A standard C++ pseudo-random number generator is created and fills the Matrix with random numbers. The numbers are set to a real distribution of -0.1 and 0.1.
The model then creates two heads representing two attention heads that each have Q, K, and V. The 3 weighted values use soft max as part of a scaled dot product process that makes up the scaled dot product and is the mathematics core of the transformer.
Final Thoughts
I hope this helps someone else, as I have struggled to find a very simplified step-by-step process for learning how the insides of
a Transformer works such that I thought to build one myself. This is how I learn best to break a system down into digestible steps and run it as a project and try and simplify it down into its smallest forms; and its how I do it to ensure I properly understood each step. I hope this hits the
right level of not being too simplified nor overly complicated.
Next Time, I am going to work through adding an optimiser. I would also eventually want to re-architect and optimise the code. There are a few places where it could simplify the process and spend less time allocating and deallocating memory with a set matrix passed between the functions but this is a learning exercise, and I do not know how far I will get with implementing the full transformer.
Add comment
Comments